- Author Jason Gerald [email protected].
- Public 2023-12-16 10:50.
- Last modified 2025-01-23 12:04.
To describe points on a coordinate plane, you must understand the arrangement of the coordinate plane and know what to do with the (x, y) coordinates. If you want to know how to represent points on the coordinate plane, just follow these steps.
Step
Method 1 of 3: Understanding Coordinate Planes

Step 1. Understand the axes of the coordinate plane
When you describe a point on the coordinate plane, you're describing it in terms of (x, y). Here are the things you need to know:
- The x-axis has a direction to the left and right, the second coordinate lies on the y-axis.
- The y-axis has an up and down direction.
- Positive numbers have an upward or rightward direction (depending on the axis). Negative numbers have a direction to the left or down.

Step 2. Understand the quadrants on the coordinate plane
Remember that a graph has four squares (usually indicated by Roman numerals). You need to know which quadrant the field is in.
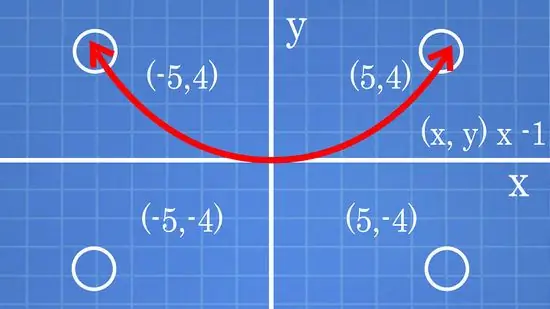
- Quadrant I has coordinates (+, +); Quadrant I is above and to the left of the x-axis.
- Quadrant IV has coordinates (+, -); Quadrant IV is below the x-axis and to the right of the y-axis. (5, 4) are in quadrant I.
- (-5, 4) is in quadrant II. (-5, -4) is in quadrant III. (5, -4) is in quadrant IV.
Method 2 of 3: Drawing a Single Point
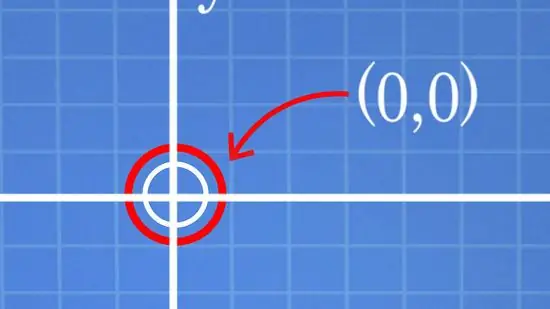
Step 1. Start at (0, 0) or origin
Go to (0, 0), which is the intersection of the x and y axes, right in the middle of the coordinate plane.
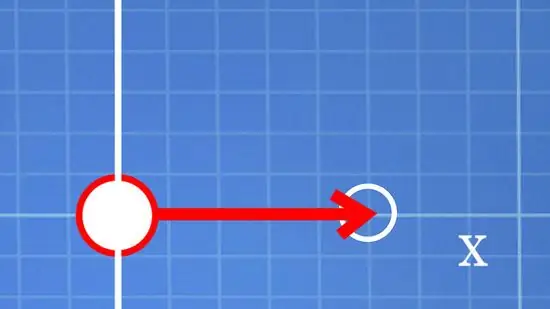
Step 2. Move x units to the right or left
Suppose you use a coordinate pair (5, -4). Your x-coordinate is 5. Since 5 is positive, you must move 5 units to the right. If the number is negative, you move it 5 units to the left.

Step 3. Move the y unit up or down
Start at your final location, 5 units to the right of (0, 0). Since your y-coordinate is -4, you must move it 4 units down. If the coordinates are 4, you move it 4 units up.

Step 4. Mark the dots
Mark the point you found by moving 5 units to the right and 4 units down, the dot (5, -4), which is in quadrant 4. You're done.
Method 3 of 3: Following Advanced Techniques
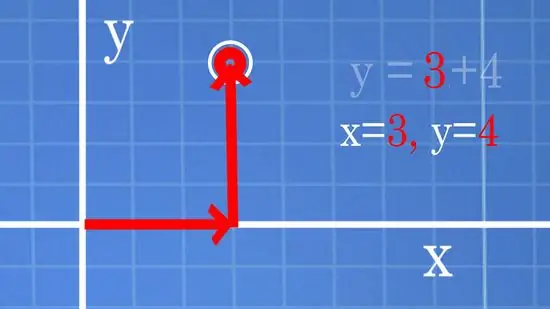
Step 1. Learn how to draw dots if you use equations
If you have a formula without any coordinates, then you have to find your points by having random coordinates for x and see the result of the formula for y. Keep looking until you find enough dots and can draw them, connecting them if necessary. Here's how you do it, whether you're using a linear line, or a more complicated equation like a parabola:
- Draw the points of a line. Let's say the equation is y = x + 4. So, pick a random number for x, such as 3, and see what results you get for y. y = 3 + 4 = 7, so you have found the point (3, 7).
- Draw the points of the quadratic equation. Let the equation of the parabola be y = x2 + 2. Do the same: pick a random number for x and see what result you get for y. Choosing 0 for x is the easiest. y = 02 + 2, so y = 2. You have found the point (0, 2).

Step 2. Connect the dots if necessary
If you have to graph a line, draw a circle, or connect all the points of another parabola or quadratic equation, then you have to connect the dots. If you have a linear equation, then draw a line connecting the points from left to right. If you are using a quadratic equation, then connect the points with a curved line.
- Unless you're only describing one point, you'll need at least two. A line requires two points.
- A circle needs two points if one of them is the center; three if the center is not included (Unless your teacher includes the center of the circle in the problem, use three).
- A parabola requires three points, one as a minimum or maximum absolute value; the other two points are the opposite.
- A hyperbola requires six points; three points on each axis.
Step 3. Understand how changing the equation will change the graph
Here are the different ways to change the equation that changes the graph:
- A change in the x-coordinate moves the equation left or right.
- Adding a constant moves the equation up or down.
- Converts to negative (multiply by -1), reverses it; if it is a line, will change it from top to bottom or from bottom to top.
- Multiplying by another number will increase or decrease the slope.
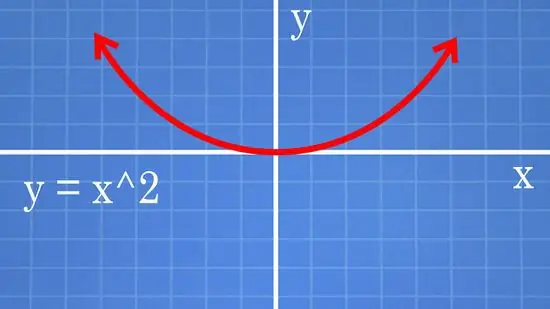
Step 4. Follow the following example to see how changing the equation changes the graph
Use the equation y = x^2; parabola with a base at (0, 0). Here's the difference you'll see when you change the equation:
- y = (x-2)^2 is the same parabola, but drawn two places to the left of the original parabola; the base is now at (2, 0).
- y = x^2 + 2 is still the same parabola, but is now drawn two places higher at (0, 2).
- y = -x^2 (negative is used after the power of ^2) is the reciprocal of y = x^2; the base is (0, 0).
- y = 5x^2 is still a parabola, but the parabola is getting bigger and faster, making it appear thinner.
Tips
- If you created this graph, you should most likely read it too. A good way to remember the x-axis is first and the y-axis second, is to imagine that you are building a house, and you have to build the foundation (along the x-axis) first before you can build. It is the same with the other directions; if you go down, imagine you are making a dungeon. You still need a foundation and start from the top.
- A good way to remember axes is to imagine the vertical axis has a small slash on its axis, making it look like a "y".
- Axes are essentially horizontal and vertical number lines, with both of them intersecting at the origin (the origin on the coordinate plane is zero, or where the two axes intersect). Everything "starts" from the origin.






