In derived calculus, an inflection point is the point on a curve at which the curve changes sign (from positive to negative or from negative to positive). It is used in a variety of subjects, including engineering, economics, and statistics, to determine fundamental changes in data. If you need to find the inflection point of a curve, go to Step 1.
Step
Method 1 of 3: Understanding Inflection Points
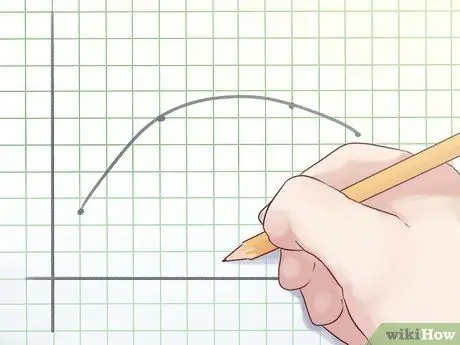
Step 1. Understand the concave function
To understand the inflection point, you need to distinguish between concave and convex functions. A concave function is a function in which the line connecting two points on the graph is never above the graph.
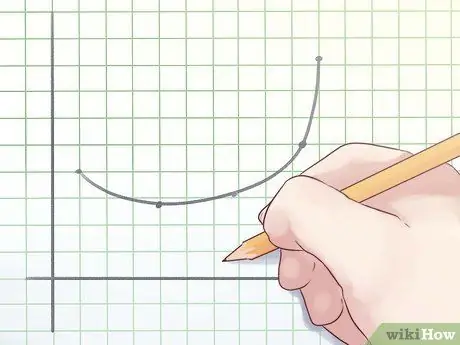
Step 2. Understand the convex function
A convex function is basically the opposite of a convex function: that is, a function in which the line connecting two points on the graph is never below the graph.
Step 3. Understand the basics of a function
The basis of a function is the point where the function is equal to zero.
If you're going to graph a function, the bases are the points where the function intersects the x-axis
Method 2 of 3: Finding the Derivative of a Function
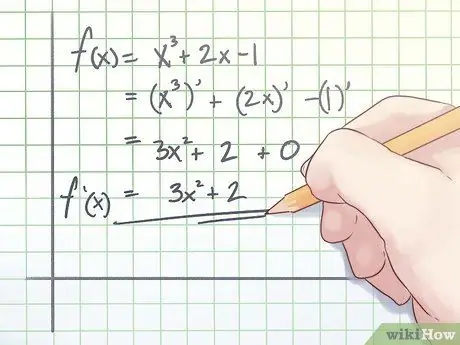
Step 1. Find the first derivative of your function
Before you can find the inflection point, you must find the derivative of your function. The derivative of the basic function can be found in any calculus book; You need to learn them before you can move on to more complicated jobs. The first derivative is written as f '(x). For a polynomial expression of the form axp + bx(p−1) + cx + d, the first derivative is apx(p−1) + b(p 1)x(p−2) + c.
-
To illustrate, suppose you have to find the inflection point of the function f(x) = x3 +2x−1. Calculate the first derivative of the function like this:
f (x) = (x3 + 2x 1)′ = (x3)′ + (2x)′ (1)′ = 3x2 + 2 + 0 = 3x2 + 2
Step 2. Find the second derivative of your function
The second derivative is the first derivative of the first derivative of the function, written as f (x).
-
In the example above, calculating the second derivative of the function would be like this:
f (x) = (3x2 + 2)′ = 2 × 3 × x + 0 = 6x
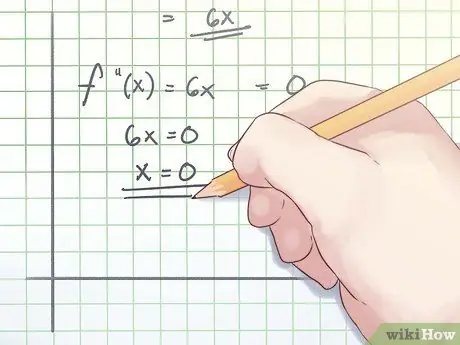
Step 3. Make the second derivative equal to zero
Set your second derivative to equal zero and solve the equation. Your answer is a possible inflection point.
-
In the example above, your calculation would look like this:
f (x) = 0
6x = 0
x=0
Step 4. Find the third derivative of your function
To see if your answer really is an inflection point, find the third derivative, which is the first derivative of the second derivative of the function, written as f (x).
-
In the example above, your calculation would look like this:
f (x) = (6x)′ = 6
Method 3 of 3: Finding Inflection Points
Step 1. Check your third derivative
The standard rule for checking possible inflection points is as follows: “If the third derivative is not zero, f (x) =/ 0, the possible inflection point is actually the inflection point.” Check your third derivative. If it is not equal to zero, then that value is the true inflection point.
In the example above, your third derivative is 6, not 0. Thus, 6 is the true inflection point
Step 2. Find the point of inflection
The coordinates of the inflection point are written as (x, f(x)), where x is the value of the variable point at the inflection point and f(x) is the function value at the inflection point.
-
In the example above, remember that when you calculate the second derivative, you find that x = 0. Thus, you must find f(0) to determine your coordinates. Your calculation will look like this:
f(0) = 03 +2×0−1 = 1.
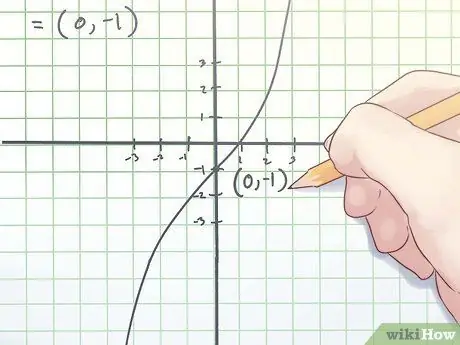
Step 3. Record your coordinates
The coordinates of your inflection point are your x-value and the value you calculated above.
