How to Derivate Implicit Functions: 7 Steps (with Pictures)

2024 Author: Jason Gerald | [email protected]. Last modified: 2024-01-19 22:11

In calculus, when you have an equation for y written in the form x (eg y = x² -3x), it is easy to use basic derivation techniques (referred to by mathematicians as implicit function derivative techniques) to find the derivative. However, for equations that are difficult to construct with only the y term on one side of the equals sign (e.g. x² + y² - 5x + 8y + 2xy² = 19), a different approach is needed. With a technique called implicit function derivatives, it's easy to find derivatives of multi-variable equations as long as you know the basics of explicit function derivatives!

Step

Method 1 of 2: Deriving Simple Equations Quickly

Step 1. Derive the x terms as usual

When trying to derive a multi-variable equation like x² + y² - 5x + 8y + 2xy² = 19, it can be difficult to know where to start. Fortunately, the first step of the derivative of an implicit function is the easiest. Just derive the x-terms and the constants on both sides of the equation according to the rules of ordinary (explicit) derivatives to begin with. Ignore the y terms for the time being.

• Let's try to derive an example of the simple equation above. x² + y² - 5x + 8y + 2xy² = 19 has two terms x: x² and -5x. If we want to derive an equation, we have to do this first, like this:

  x² + y² - 5x + 8y + 2xy² = 19

  (Bring down to the power of 2 in x² as coefficient, remove x in -5x, and change 19 to 0)

  2x + y² - 5 + 8y + 2xy² = 0

Step 2. Derive the y terms and add (dy/dx) next to each term

For your next step, just derive the y terms the same way you derived the x terms. This time, however, add (dy/dx) next to each term as you would add coefficients. For example, if you lower y², then the derivative becomes 2y(dy/dx). Ignore the terms that have x and y for the time being.

• In our example, our equation now looks like this: 2x + y² - 5 + 8y + 2xy² = 0. We will perform the next step of deriving y as follows:

  2x + y² - 5 + 8y + 2xy² = 0

  (Bring down to the power of 2 in y² as coefficients, remove y in 8y, and put dy/dx next to each term).

  2x + 2y(dy/dx) - 5 + 8(dy/dx) + 2xy²= 0

Step 3. Use the product rule or the quotient rule for terms having x and y

Working with terms that have x and y is a bit tricky, but if you know the rules for the product and quotient for derivatives, you'll find it easy to do. If the terms x and y are multiplied, use the product rule ((f × g)' = f' × g + g × f'), substituting the x term for f and the y term for g. On the other hand, if the terms x and y are mutually exclusive, use the quotient rule ((f/g)' = (g × f' - g' × f)/g²), substituting the numerator for f and the denominator for g.

• In our example, 2x + 2y(dy/dx) - 5 + 8(dy/dx) + 2xy² = 0, we have only one term which has x and y - 2xy². Since x and y are multiplied by each other, we will use the product rule to derive as follows:

  2xy² = (2x)(y²)- set 2x = f and y² = g in (f × g)' = f' × g + g × f'

  (f × g)' = (2x)' × (y²) + (2x) × (y²)'

  (f × g)' = (2) × (y²) + (2x) × (2y(dy/dx))

  (f × g)' = 2y² + 4xy(dy/dx)

• Adding this to our main equation, we get 2x + 2y(dy/dx) - 5 + 8(dy/dx) + 2y² + 4xy(dy/dx) = 0

Step 4. Alone (dy/dx)

You're almost done! Now, all you have to do is solve the equation (dy/dx). This seems difficult, but it usually isn't - remember that any two terms a and b are multiplied by (dy/dx) can be written as (a + b)(dy/dx) because of the distributive property of multiplication. This tactic can make isolating (dy/dx) easier - just move all the other terms on the other side of the parentheses, then divide by the terms in the parentheses next to (dy/dx).

• In our example, we simplify 2x + 2y(dy/dx) - 5 + 8(dy/dx) + 2y² + 4xy(dy/dx) = 0 as follows:

  2x + 2y(dy/dx) - 5 + 8(dy/dx) + 2y² + 4xy(dy/dx) = 0

  (2y + 8 + 4xy)(dy/dx) + 2x - 5 + 2y² = 0

  (2y + 8 + 4xy)(dy/dx) = -2y² - 2x + 5

  (dy/dx) = (-2y² - 2x + 5)/(2y + 8 + 4xy)

  (dy/dx) = (-2y² - 2x + 5)/(2(2xy + y + 4)

Method 2 of 2: Using Advanced Techniques

Step 1. Enter the value (x, y) to find (dy/dx) for any point

Safe! You've implicitly derived your equation - not an easy job on the first try! Using this equation to find the gradient (dy/dx) for any point (x, y) is as easy as plugging the x and y values for your point to the right side of the equation, then finding (dy/dx).

• For example, suppose we want to find the gradient at the point (3, -4) for our example equation above. To do so, we'll substitute 3 for x and -4 for y, solving as follows:

  (dy/dx) = (-2y² - 2x + 5)/(2(2xy + y + 4)

  (dy/dx) = (-2(-4)² - 2(3) + 5)/(2(2(3)(-4) + (-4) + 4)

  (dy/dx) = (-2(16) - 6 + 5)/(2(2(3)(-4))

  (dy/dx) = (-32) - 6 + 5)/(2(2(-12))

  (dy/dx) = (-33)/(2(2(-12))

  (dy/dx) = (-33)/(-48) = 3/48, or 0, 6875.

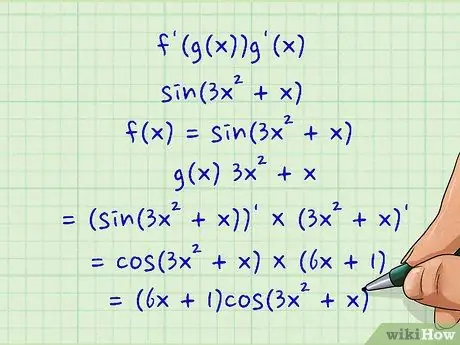
Step 2. Use the chain rule for functions-within-functions

The chain rule is an important piece of knowledge to have when working on calculus problems (including implicit function derivative problems). The chain rule states that for a function F(x) which can be written as (f o g)(x), the derivative of F(x) is equal to f'(g(x))g'(x). For difficult implicit function derivative problems, this means that it is possible to derive the different individual parts of the equation, and then combine the results.

• As a simple example, suppose we have to find the derivative of sin(3x² + x) as part of the larger implicit function derivative problem for the equation sin(3x² +x) + y³ = 0. If we imagine sin(3x² + x) as f(x) and 3x² + x as g(x), we can find the derivative as follows:

  f'(g(x))g'(x)

  (sin(3x² + x))' × (3x² +x)'

  cos(3x² +x) × (6x + 1)

  (6x + 1)cos(3x² +x)

Step 3. For equations with the variables x, y, and z, find (dz/dx) and (dz/dy)

Although unusual in basic calculus, some advanced applications may require the derivation of implicit functions of more than two variables. For each additional variable, you must find its additional derivative with respect to x. For example, if you have x, y, and z, you should search for both (dz/dy) and (dz/dx). We can do this by deriving the equation with respect to x twice - first, we'll insert (dz/dx) every time we derive a term containing z, and second, we'll insert (dz/dy) every time we derive z. After this, it's just a matter of resolving (dz/dx) and (dz/dy).

• For example, let's say we are trying to derive x³z² - 5xy⁵z = x² + y³.

• First, let's derive against x and enter (dz/dx). Don't forget to apply the product rule if needed!

  x³z² - 5xy⁵z = x² + y³

  3x²z² + 2x³z(dz/dx) - 5y⁵z - 5xy⁵(dz/dx) = 2x

  3x²z² + (2x³z - 5xy⁵)(dz/dx) - 5y⁵z = 2x

  (2x³z - 5xy⁵)(dz/dx) = 2x - 3x²z² + 5y⁵z

  (dz/dx) = (2x - 3x²z² + 5y⁵z)/(2x³z - 5xy⁵)

• Now, do the same for (dz/dy)

  x³z² - 5xy⁵z = x² + y³

  2x³z(dz/dy) - 25xy⁴z - 5xy⁵(dz/dy) = 3y²

  (2x³z - 5xy⁵)(dz/dy) = 3y² + 25xy⁴z

  (dz/dy) = (3y² + 25xy⁴z)/(2x³z - 5xy⁵)