- Author Jason Gerald [email protected].
- Public 2024-01-15 08:07.
- Last modified 2025-06-01 06:05.
A trinomial is an algebraic expression consisting of three terms. Most likely, you will begin to learn how to factor a quadratic trinomial, meaning a trinomial written in the form ax2 + bx + c. There are a few tricks to learn, which can be used for many different types of quadratic trinomials, but you'll be able to use them better and faster with practice. Higher order polynomials, with terms like x3 or x4, can't always be solved in the same way, but you can often use simple factoring or substitution to turn it into a problem that can be solved like any other quadratic formula.
Step
Method 1 of 3: Factoring x2 + bx + c
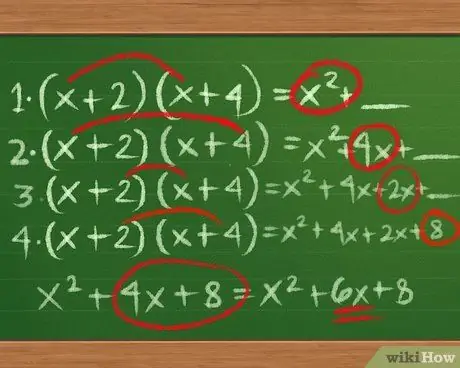
Step 1. Learn PLDT multiplication
You may have learned how to multiply PLDT, or "First, Outside, In, Last" to multiply expressions like (x+2)(x+4). It's useful to know how this multiplication works before we factor:
- Multiply the tribes First: (x+2)(x+4) = x2 + _
-
Multiply the tribes Outside: (x+2)(x+
Step 4.) = x2+ 4x + _
-
Multiply the tribes In: (x+
Step 2.)(x+4) = x2+4x+ 2x + _
-
Multiply the tribes Final: (x+
Step 2.)(x
Step 4.) = x2+4x+2x
Step 8.
- Simplify: x2+4x+2x+8 = x2+6x+8
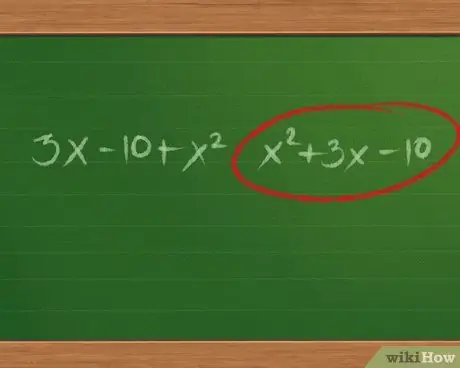
Step 2. Understand factoring
When you multiply two binomials using the PLDT method, you get a trinomial (an expression with three terms) in the form a x2+ b x+ c, where a, b, and c are ordinary numbers. If you start with an equation that has the same form, you can factor it back into two binomials.
- If the equations are not written in this order, rearrange the equations so that they have this order. For example, rewrite 3x - 10 + x2 Becomes x2 + 3x - 10.
- Because the highest power is 2 (x2, this type of expression is called quadratic.

Step 3. Leave a blank space for the answer in the form of PLDT multiplication
For now, just write (_ _)(_ _) where you will write the answer. We will fill it while working on it
Don't write + or - between the empty terms because we don't know the correct sign yet

Step 4. Fill in the first terms
For simple problems, the first term of your trinomial is just x2, the terms in the First position are always x and x. These are the factors of the term x2 because x times x = x2.
- Our example x2 + 3x - 10 starting with x2, so we can write:
- (x _)(x _)
- We'll work on more complex problems in the next section, including trinomials starting with terms like 6x2 or -x2. In the meantime, follow these sample questions.
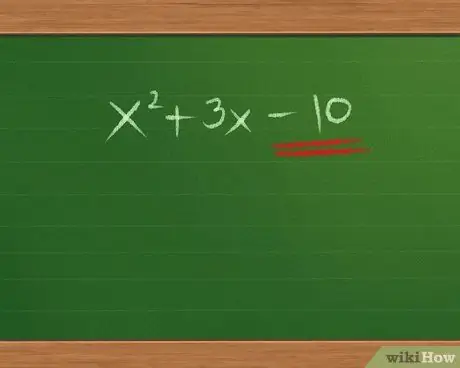
Step 5. Use factoring to guess the Last terms
If you go back and read the steps for how to multiply PLDT, you'll see that multiplying the Last terms will produce the last term in the polynomial (terms that don't have x). So to factor, we have to find two numbers which when multiplied will produce the last term.
- In our example x2 + 3x - 10, the last term is -10.
- What are the factors of -10? What number is multiplied by -10?
- There are several possibilities: -1 times 10, 1 times -10, -2 times 5, or 2 times -5. Write these pairs down somewhere to remember them.
- Don't change our answer just yet. Our answer should still look like this: (x _)(x _).
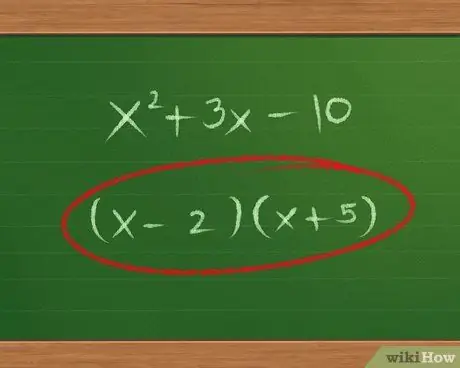
Step 6. Test the possibilities that match the Outer and Inner product
We've narrowed the Last terms down to a few possibilities. Use the trial system to test every possibility, multiplying the Outer and Inner terms and comparing the product with our trinomial. For example:
- Our original problem had the term "x" at 3x, so our test results should match this term.
- Tests -1 and 10: (x-1)(x+10). Outside + Inside = 10x - x = 9x. Wrong.
- Tests 1 and -10: (x+1)(x-10). -10x + x = -9x. This is wrong. In fact, if you test -1 and 10, you'll find that 1 and -10 are the opposite of the answer above: -9x instead of 9x.
- Tests -2 and 5: (x-2)(x+5). 5x - 2x = 3x. The result corresponds to the initial polynomial, so here's the correct answer: (x-2)(x+5).
- In simple cases like this, if you don't have a constant in front of the term x2, you can use the quick way: just add up the two factors and put an "x" behind it (-2+5 → 3x). However, this method doesn't work for more complex problems, so it's better to remember the "long way" described above.
Method 2 of 3: Factoring More Complex Trinomials

Step 1. Use simple factoring to make more complex problems simpler
For example, you have to factor 3x2 + 9x - 30. Find a number that can factor all three terms ("greatest common factor" or GCF). In this case, the GCF is 3:
- 3x2 = (3)(x2)
- 9x = (3)(3x)
- -30 = (3)(-10)
- Thus, 3x2 + 9x - 30 = (3)(x2+3x-10). We can factor out the new trinomial using the steps in the section above. Our final answer will be (3)(x-2)(x+5).

Step 2. Look for more complicating factors
Sometimes, the factoring may involve a variable, or you may need to factor several times to find the simplest possible expression. Here are some examples:
- 2x2y + 14xy + 24y = (2y)(x2 + 7x + 12)
- x4 + 11x3 - 26x2 = (x2)(x2 +11x - 26)
- -x2 + 6x - 9 = (-1)(x2 - 6x + 9)
- Don't forget to refactor the new trinomial, using the steps in Method 1. Check your work and look for examples of similar problems in the sample questions near the bottom of this page.

Step 3. Solve problems with a number in front of x2.
Some quadratic trinomials cannot be reduced to the easiest type of problem. Learn how to solve problems like 3x2 + 10x + 8, then practice on your own with the sample questions at the bottom of this page:
- Set our answer to be: (_ _)(_ _)
- Our "First" terms will each have one x, and multiplying them gives 3x2. There is only one possibility: (3x _)(x _).
- List the factors of 8. The odds are 1 times 8 or 2 times 4.
- Test this possibility using the Outer and Inner terms. Note that the order of the factors is very important because the Outer term is multiplied by 3x instead of x. Try every possibility until you get Out+In = 10x (from the original problem):
- (3x+1)(x+8) → 24x+x = 25x no
- (3x+8)(x+1) → 3x+8x = 11x no
- (3x+2)(x+4) → 12x+2x=14x no
- (3x+4)(x+2) → 6x+4x=10x yes. This is the correct factor.

Step 4. Use substitution for higher order trinomials
Your math book may surprise you with equations with high powers, such as x4, even after you use simple factoring to make the problem easier. Try substituting a new variable that turns it into a problem you know how to solve. For example:
- x5+13x3+36x
- =(x)(x4+13x2+36)
- Let's create a new variable. Let's say y = x2 and put in it:
- (x)(y2+13y+36)
- =(x)(y+9)(y+4). Now, convert it back to the initial variable:
- =(x)(x2+9)(x2+4)
- = (x)(x±3)(x±2)
Method 3 of 3: Factoring Special Cases
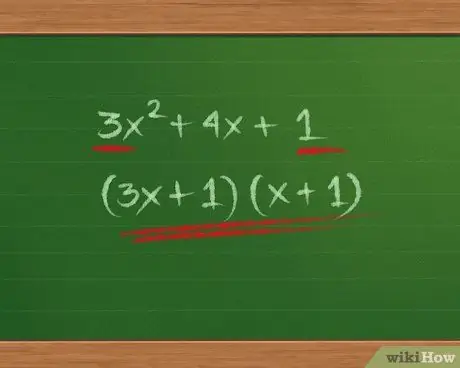
Step 1. Find prime numbers
Look to see if the constant in the first or third term of the trinomial is a prime number. A prime number is only divisible by itself and 1, so there is only one possible pair of binomial factors.
- For example, in x2 + 6x + 5, 5 is a prime number, so the binomial must be of the form (_ 5)(_ 1).
- In the problem of 3x2+10x+8, 3 is a prime number, so the binomial must be of the form (3x _)(x _).
- For questions 3x2+4x+1, both 3 and 1 are prime numbers, so the only possible solution is (3x+1)(x+1). (You should still multiply this number to check your answer because some expressions cannot be factored at all - for example, 3x2+100x+1 has no factor.)
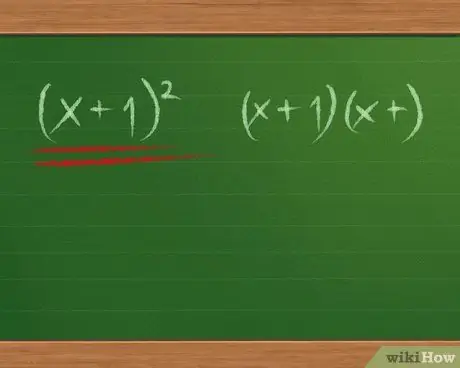
Step 2. Find out if the trinomial is a perfect square
A perfect square trinomial can be factored into two identical binomials, and the factor is usually written as (x+1)2 and not (x+1)(x+1). Here are some examples that tend to appear in questions:
- x2+2x+1=(x+1)2, and x2-2x+1=(x-1)2
- x2+4x+4=(x+2)2, and x2-4x+4=(x-2)2
- x2+6x+9=(x+3)2, and x2-6x+9=(x-3)2
- Perfect square trinomial in the form a x2 + bx + c always has terms a and c that are positive perfect squares (such as 1, 4, 9, 16, or 25) and one term b (positive or negative) which is equal to 2(√a * √c).
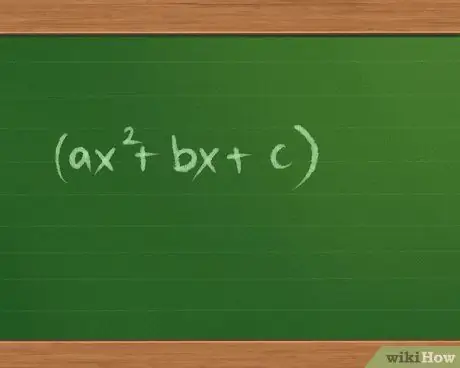
Step 3. Find out if a problem has no solution
Not all trinomials can be factored. If you cannot factor a quadratic trinomial (ax2+bx+c), use the quadratic formula to find the answer. If the only answer is the square root of a negative number, there is no real number solution, then the problem has no factors.
For non-square trinomials, use the Eisenstein Criterion, which is described in the Tips section
Answers and Example Questions
-
Answers to "complicated factoring" questions.
These are questions from the "more complicated factors" step. We've simplified the problems into easier ones, so try to solve them using the steps in method 1, then check your work here:
- (2y)(x2 + 7x + 12) = (x+3)(x+4)
- (x2)(x2 + 11x - 26) = (x+13)(x-2)
- (-1)(x2 - 6x + 9) = (x-3)(x-3) = (x-3)2
-
Try more complex factoring problems.
These problems have the same factor in each term which must be factored first. Block the blanks after the equals sign to see the answers so you can check your work:
- 3x3+3x2-6x = (3x)(x+2)(x-1) block the blank to see the answer
- -5x3y2+30x2y2-25y2x = (-5xy^2)(x-5)(x-1)
-
Practice using questions. These problems can't be factored into easier equations, so you'll have to find the answer in the form (_x + _)(_x + _) using trial and error:
- 2x2+3x-5 = (2x+5)(x-1) block to see the answer
- 9x2+6x+1 = (3x+1)(3x+1)=(3x+1)2 (Hint: You may want to try more than one factor pair for 9x.)
Tips
- If you can't figure out how to factor a quadratic trinomial (ax2+bx+c), you can use the quadratic formula to find x.
-
While you don't need to know how to do this, you can use the Eisenstein Criteria to quickly determine if a polynomial cannot be simplified and factored. This criterion applies to any polynomial but is best used for trinomials. If there is a prime number p that divides the last two terms evenly and satisfies the following conditions, then the polynomial cannot be simplified:
- Constant terms (without variables) are multiples of p but not multiples of p2.
- The prefix (for example, a in ax2+bx+c) is not a multiple of p.
- For example, 14x2 +45x +51 cannot be simplified because there is a prime number (3) which can evenly divide both 45 and 51, but not divisible by 14, and 51 is not divisible by 32.
Warning
While this is true for quadratic trinomials, the trinomial that can be factored is not necessarily the product of two binomials. For example, x4 + 105x + 46 = (x2 + 5x + 2)(x2 - 5x + 23).






