- Author Jason Gerald gerald@how-what-advice.com.
- Public 2024-02-01 14:11.
- Last modified 2025-01-23 12:04.
The process of determining the squared inch (written as in2) in all areas of two-dimensional figures are usually quite simple. For the simplest case, when the figure is a square or quadrilateral, the area in inches squared can be obtained using the formula length × width.
The areas of other plane shapes (circles, triangles, etc.) can be calculated by various mathematical formulas. You can also do a simple conversion of feet squared or centimeters squared from inches squared, if needed.
Step
Method 1 of 3: Determining Square Inches on a Square or Square
Step 1. Determine the length of the area to be measured
Squares and rectangles have 4 straight sides. A square has four sides that are the same length, whereas in a rectangle, only the opposite sides are the same length. Measure one of the sides of the square or rectangle to find out the length value.
Step 2. Determine the width of the area to be measured
Next, measure one of the sides next to the side previously measured. This side should meet the first side at a 90 degree angle. This is the width of your square or rectangle.
Since all four sides of the square are the same length, the resulting "length" will be equal to the "width" measure. So, usually for a square you only need to measure one side
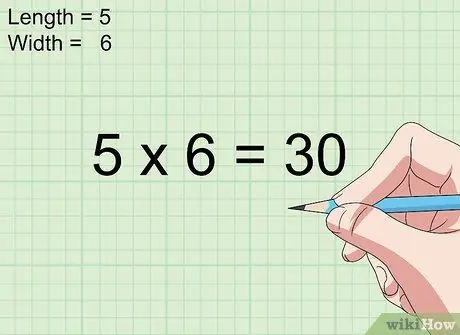
Step 3. Multiply the length and the width
Simply multiply the length and width measurements to determine the area of a square or rectangle in inches squared.
- For example, say that the problem asks for the area of a rectangle that is 4 inches long and 3 inches wide. In this case, the area of the rectangle is 4 x 3 = 12 inches squared.
- Again, all sides of the square have the same side length. So you only need to measure one side and multiply it by the number itself (also known as "squaring" or to the power of two) to get the area in inches squared.
Method 2 of 3: Determining Square Inches on Other Flat Shapes
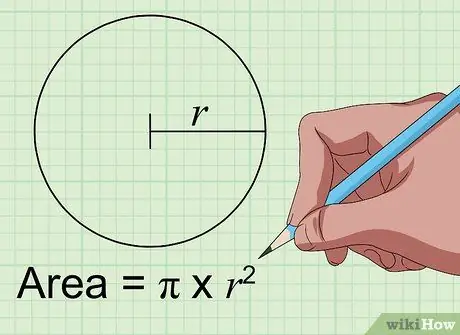
Step 1. Find the area of a circle using the formula Area = pi × r2.
To find the area of a circle in inches squared, you only need to know the distance from the center of the circle to its sides in inches. This distance is called the "radius" of the circle. Once you've got it, just plug the number into the variable "r" in the formula above. Multiply by the number itself, then multiply by the constant pi (3, 1415926…) to get the area of the circle in inches squared.
So, a circle with a radius of 4 inches has an area of 50.27 inches squared which is the product of 3.14 x 16
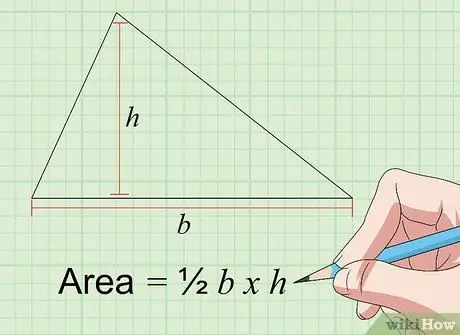
Step 2. Find the area of the triangle using the formula Area = 1/2 a × t
The area of a triangle in inches squared can be found by multiplying the base ("a") and the height ("t"), both of which are in inches. The base of a triangle is the length of one of its sides, while the "height" of a triangle is the distance from the side of the "base" to the corner of the triangle opposite it at a 90-degree angle. The area of a triangle can be calculated if you know the lengths of the sides of the base and the heights of the three sides and the angles opposite them.
Thus, if you choose a side that is 4 inches long as the base, and the height of that side of the base is 3 inches, the area of the triangle is 2 x 3 = 6 inches squared
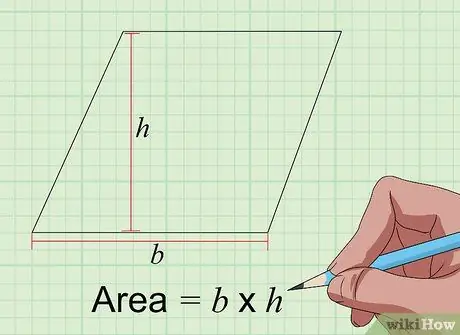
Step 3. Find the area of the parallelogram with the formula Area = a × t
A parallelogram is similar to a rectangle, but the sides don't meet at a 90-degree angle. However, the way to find the area of a parallelogram in inches squared is the same as that of a rectangle, by multiplying the base by the height in inches. The base is the length of one of its sides, while the height is the distance from the side of the base to the opposite side at an angle of 90 degrees.
Therefore, if the length of the selected side is 5 inches, and after measuring the height it is 4 inches long, the area is 5 x 4 = 20 inches squared
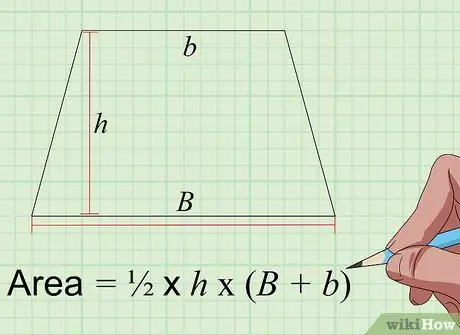
Step 4. Find the area of the trapezoid using the formula Area = 1/2 × t × (A+a)
A trapezoid is a 4-sided flat shape with one pair of parallel sides and the other non-parallel sides. To calculate the area of a trapezoid in inches squared, you need to know 3 measurements in inches, respectively, the length of the long parallel side (“A”), the shorter parallel side (“a”), and the height of the trapezoid (“t”)., i.e. the distance between two parallel sides measured in 90 degree angles. Add the lengths of the two parallel sides, multiply by the height, then divide by two to get the area of the trapezoid in inches squared.
For example, if the parallel sides of a trapezoid are 6 inches long, the short parallel sides are 4 inches, and the height is 5 inches, the area is x 5 x (6+4) = 25 square inches
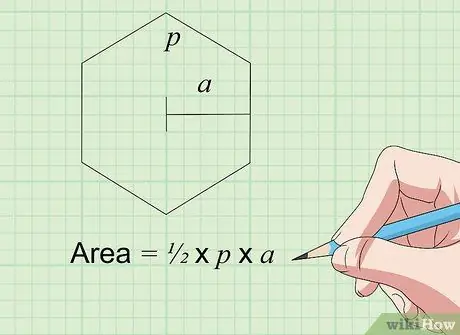
Step 5. Find the area of the hexagon (hexagon) with the formula Area = × K × s
This formula works for all regular hexagons, which are flat shapes that have 6 equal sides and 6 equal angles. K is the perimeter, or side length times 6 (6 x s) for a regular hexagon. The variable a represents the apothem, which is the length from the center of the hexagon to one of its sides (the midpoint of the side between the two angles). Multiply and divide the result by two to find the area of the hexagon.
Thus, if a hexagon with all six sides is 4 inches long (which means K = 6 x 4 = 24) and the apothem is 3.5 inches long, the area is x 24 x 3.5 = 42 square inches
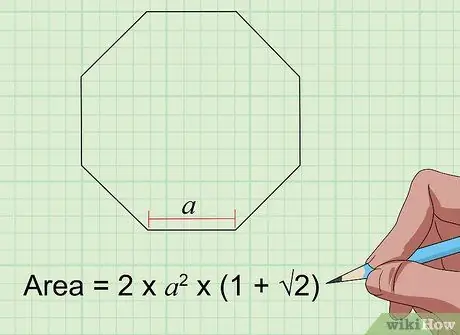
Step 6. Find the area of the octagon with the formula Area = 2s² × (1 + 2)
For a regular octagon (which has 8 equal sides and 8 angles), you only need to know the length of one side (“s” in the formula) to find the area. Plug the values into the formula and work them out to get the area of the octagon.
If your regular octagon has a side length of 4 inches, its area is 2(16) x (1 + 1, 4) = 32 x 2.4 = 76.8 square inches
Method 3 of 3: Converting Other Units to Square Inches

Step 1. Resize to inches before you count
To get a final answer in inches squared, we recommend converting all values to be calculated into inches (such as length, height, or apothem). Thus, if the sides of the square are 1 foot each, convert them to 12 inches before calculating the area. The following conversion factors are commonly used to convert to inches:
- 1 foot = 12 inches
- 1 yard = 36 inches
- 1 centimeter = 0.3937 inch
- 1 meter = 39.3701 inches
- 1 millimeter = 0.0394 inch
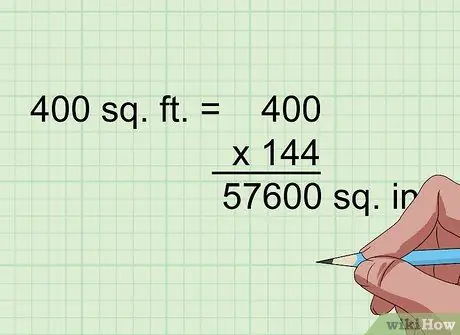
Step 2. Multiply by 144 to convert squared feet to squared inches
1 foot squared is 1 foot squared (1 foot times 1 foot); which means, 12 inches squared also equals 12 inches times 12 inches, which makes 144 inches squared. So, if a flat shape has area in feet squared, simply multiply it by 144 to convert it to inches squared.
For example, 400 feet squared = 400 x 144 = 57,600 inches squared
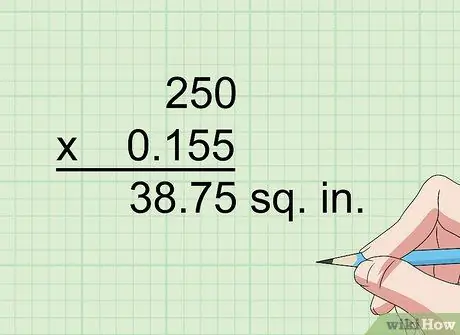
Step 3. Multiply by 0.155 to convert squared centimeters to squared inches
One centimeter equals 0.394 inches, and 0.394 squared (0.394 x 0.394) equals 0.155. So, for example, if you need to convert 250 centimeters squared to inches squared, multiply 250 by 0.155 to get 38.75 inches squared.






