- Author Jason Gerald [email protected].
- Public 2023-12-16 10:50.
- Last modified 2025-01-23 12:04.
Geometry is the science of shapes and angles. Learning this science may seem difficult for many students. There are many concepts that are new in geometry and they can be daunting for students. You must study postulates, definitions, and symbols in order to understand geometry. If you combine good study habits and a few tips on geometry, you can master geometry.
Step
Part 1 of 3: Getting Score

Step 1. Attend each class
Classroom is a place to learn new things and reinforce information you may have learned in previous classes. If you don't attend class, you will find it difficult to keep up with the latest material.
- Ask in class. Your teacher must make sure that you really understand the material that has been taught. If you have any questions, don't hesitate to ask them. Some of the other students in the class may have the same question as you.
- Before entering class, read the material to be taught and memorize formulas, propositions, and postulates.
- Watch your teacher in class. Talk to your friends only during recess or after school.
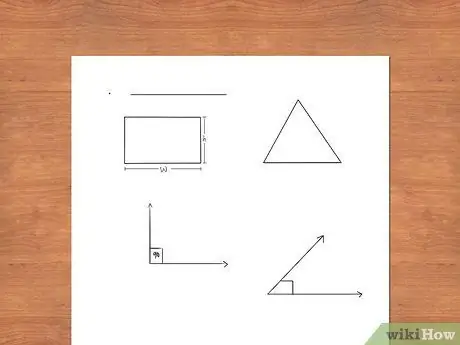
Step 2. Draw a diagram
Geometry is the mathematics of shapes and angles. To understand geometry, it will be easier if you visualize the problem and draw diagrams. If you are asked about the angle, draw it. The relationships of the vertical angles will be easier to see in the diagram. If a diagram is not provided, draw it.
- Understanding the properties of shapes and visualizing them are important components of mastering geometry.
- Practice recognizing shapes in various orientations and based on their geometric characteristics (angle measure, number of parallel and parallel lines, etc.)

Step 3. Form study groups
Study groups are a good way to study material and clarify concepts you don't understand. Having study groups that meet regularly will force you to read and understand current material. Studying with classmates can be useful when you are dealing with more difficult topics. You can study and understand it together.
One of your friends may understand material you don't understand and can help you. You might also be able to help your friend understand something and eventually master the material better while teaching them

Step 4. Know how to use a protractor
A protractor is a semicircular tool used to measure angles. This tool can also be used to draw corners. Knowing how to use a protractor properly is an important skill in learning geometry. To measure the size of an angle:
- Place the center hole of the protractor right at the vertex of the corner.
- Rotate the protractor until the bottom line is directly above one of the legs forming the angle.
- Extend the other leg all the way to the top of the protractor and note the degree to which the angle's leg falls. This is the result of the angle measurement.

Step 5. Do all assignments and homework
Homework is used to help you understand all the concepts in the material. Doing homework will make you aware of what concepts you already understand and what topics you need to learn more about.
If you find it difficult to understand a certain topic in public relations, concentrate on that topic until you really understand it. Ask your classmate or teacher for help

Step 6. Teach the material
When you really understand a certain topic or concept, you should be able to explain it to others. If you can't explain it until someone else understands, chances are you don't understand it either. Teaching other people the material is also a good way to sharpen your memory.
- Try teaching your siblings or parents about geometry.
- Go ahead and explain concepts that you really understand when studying in groups.

Step 7. Do the practice questions
Mastering geometry requires knowledge and skills. Learning the rules of geometry without doing practice problems is not enough to get an A. You should do your homework and practice questions about concepts you don't understand.
- Make sure you do as many practice questions as possible from a variety of sources. Similar questions can be presented in different ways and may be easier for you to understand.
- The more problems you work on, the easier it will be for you to solve them next time.

Step 8. Ask for additional help
Sometimes going to class and talking to the teacher is not enough. You may need a tutor who can devote time to topics that are difficult for you to understand. Studying with someone individually can be beneficial for understanding difficult material.
- Ask your teacher if there are any tutors available at the school.
- Attend additional tutorial sessions provided by your teacher and ask your questions in the class.
Part 2 of 3: Learning Geometry Concepts
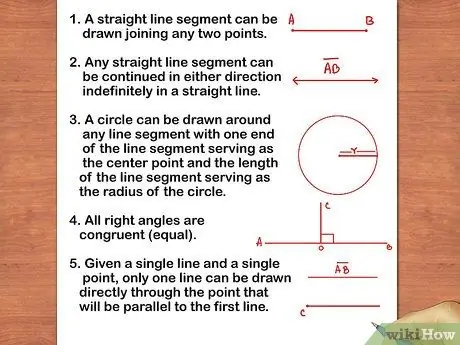
Step 1. Learn Euclid's Five Postulates of Geometry
Geometry is based on five postulates made by the ancient mathematician, Euclid. Knowing and understanding these five statements will help you learn various concepts in geometry.
- 1: A straight line can be drawn connecting any two points.
- 2: Any straight line can be continued indefinitely in any direction.
- 3. A circle can be drawn around a line with one point serving as the midpoint and the length of the line as the radius of the circle.
- 4. All right angles are congruent
- 5. If there is a line and a point, only one other line can be drawn across that point and parallel to the first line.

Step 2. Identify symbols used in geometry problems
When you're first learning, the various symbols can be confusing. Learning the meaning of each symbol and being able to recognize it quickly will make the learning process easier. Below are some of the symbols commonly used in geometry:
- The small triangle symbol represents a characteristic triangle.
- The small corner symbol describes the characteristics of a corner.
- A row of letters with a line above them represents the characteristics of a line segment.
- A row of letters with a line marked with an arrow above it describes the characteristics of a line.
- One horizontal line with a vertical line in the middle means two lines are perpendicular to each other.
- Two vertical lines means one line parallel to one other line.
- An equal sign plus a squiggly line above it means two congruent planes.
- A squiggly line means that the two shapes have almost the same shape.
- The three points that make up a triangle mean "therefore".

Step 3. Understand the characteristics of the line
A straight line can be extended to infinity in both directions. A line drawn with an arrow symbol at the end means that the line can be extended continuously. A line segment has a starting and ending point. Another form of line is called a ray: it can only be extended in one direction. The lines can be placed parallel, perpendicular, or intersect.
- Two lines parallel to each other cannot intersect.
- Two perpendicular lines form an angle of 90°.
- A crossed line is two lines that intersect each other. The intersecting lines may be perpendicular, but cannot be parallel.

Step 4. Know the different types of angles
There are three types of angles: obtuse, acute, and perpendicular. An obtuse angle is an angle that is greater than 90°; An acute angle is an angle that is less than 90°, and a perpendicular angle is an angle that measures exactly 90°. Being able to identify angles is one of the important things in studying geometry.
An angle of 90° is a perpendicular angle: two lines form a perfect angle

Step 5. Understand the Pythagorean Theorem
The Pythagorean Theorem states2 + b2 = c2. This is a formula that calculates the length of the hypotenuse of a right triangle if you already know the lengths of the other two sides. A right triangle is a triangle in which one of the angles is a perfect 90°. In the theorem, a and b are opposite and are perpendicular sides of the triangle, while c is the hypotenuse of the triangle.
- Example: Calculate the length of the hypotenuse of a right triangle if a = 2 and b = 3.
- a2 + b2 = c2
- 22 + 32 = c2
- 4 + 9 = c2
- 13 = c2
- c = 13
- c = 3, 6

Step 6. Master how to identify the types of triangles
There are three types of triangles: arbitrary, isosceles, and equilateral. None of the three sides of a triangle are the same length. An isosceles triangle has two equal sides and two equal angles. An equilateral triangle has three equal sides and three equal angles. By knowing the types of triangles, you can identify the characteristics and postulates associated with each triangle.
- Remember, an equilateral triangle can also technically be called an isosceles triangle because it has two sides that are the same length. All equilateral triangles are isosceles triangles, but not all isosceles triangles are equilateral triangles.
- Triangles can also be grouped according to the size of the angles: acute, right, and obtuse. An acute triangle has angles less than 90°; an obtuse triangle has an angle greater than 90°.
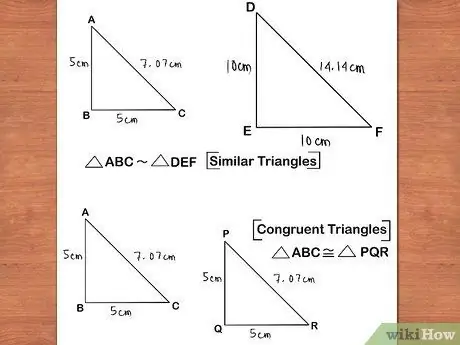
Step 7. Know the difference between similar and congruent (similar and congruent)
Similar shapes are shapes that have identical angles, but whose side lengths are proportionally smaller or larger. In other words, polygons have the same angles, but different side lengths. Congruent shapes mean the same and congruent; These shapes have the same angles and side lengths.
Comparable angles are angles that have identical angle degrees in two figures. In a right triangle, the angles of 90 degrees in the two triangles are proportional. In order to have comparable angles, the shapes do not need to have the same side size
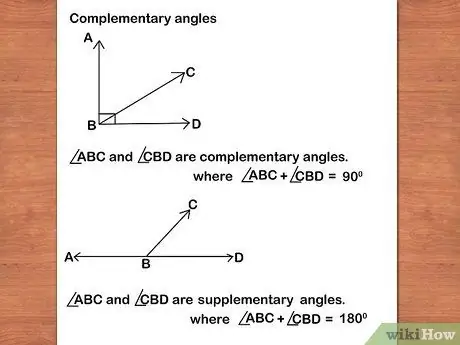
Step 8. Learn about complementary and supplementary angles
Complementary angles are angles which add up to 90 degrees, while supplementary angles add up to 180 degrees. Remember that vertical angles are always congruent; interior corners and exterior corners that are opposite are always congruent. A right angle is 90 degrees, while a straight line has an angle of 180 degrees.
- A vertical angle is two opposite angles formed by two intersecting lines.
- Interior angles are formed when two lines are intersected by a third line. The angles are on opposite sides of the third line; on the inside (interior) of the first and second lines.
- Exterior angles are also formed when two lines intersect with a third line. The angles are on opposite sides of the third line; but on the outside (exterior) of the first and second lines.
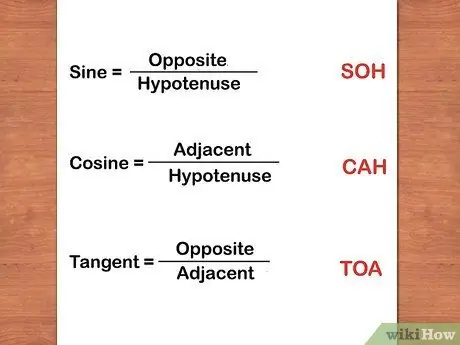
Step 9. Remember RING-FIRE-VILLAGE
RING-FIRE-VILLAGE is a mnemonic tool that can help you remember the formulas for the sine, cosine, and tangent of a right triangle. When you will calculate the sine, cosine, and tangent, use the following formula. Sine = FRONT/SIRING (ring), Cosine = SIDE/SIDE (strain), Tangen = FRONT/SIRING (village).
- Example: Calculate the sine, cosine, and tangent of the angle 39° of a right triangle with side lengths AB = 3, BC = 5 and AC = 4.
- sin(39°) = forward/skew = 3/5 = 0, 6
- cos(39°) = side/slope = 4/5 = 0, 8
- tan(39°) = front/side = 3/4 = 0.75
Part 3 of 3: Writing 2 Column Proofs
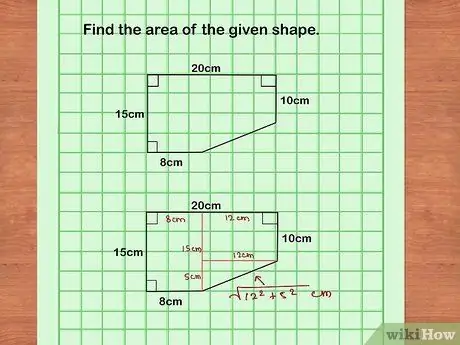
Step 1. Draw a diagram after reading the problem
Sometimes geometry problems are given without pictures and you have to draw a diagram to visualize the proof. After you've made a rough sketch that fits the problem, you may have to redraw the diagram so you can read the details clearly and the angles you're making are more or less precise.
- Make sure you label it clearly based on the information provided.
- The clearer the diagram you make, the easier it will be for you to solve the problem.
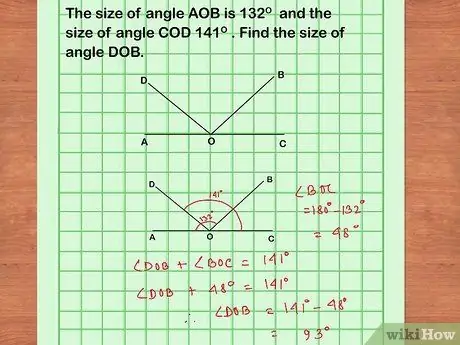
Step 2. Observe the diagram you created
Label the right angles and equal-length sides. If one line is parallel to another, write a label to describe it. If a problem doesn't explicitly state that two lines are proportional, can you prove that the two lines are proportional? Make sure you can prove all the assumptions you use.
- Write down the relationships between the lines and angles that you can conclude based on your diagram and assumptions.
- Write down all the instructions given in the problem. In proving geometry, there will be some information given by the problem. Writing down all the instructions given by the problem will help you complete the proof.
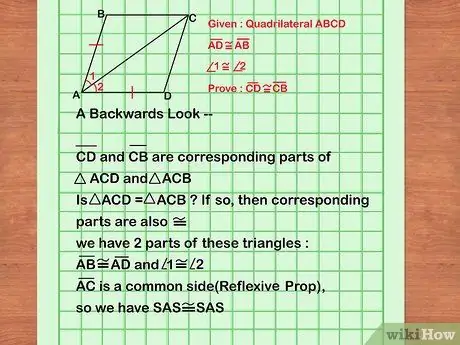
Step 3. Work from back to front
When you try to prove something in geometry, you will be given several statements about shapes and angles, then you have to prove why those statements are true. Sometimes, the easiest way to do this is to start at the end of the problem.
- How can you conclude about this?
- Are there any clear steps you have to prove to reach that conclusion?

Step 4. Create a two-column box labeled "Statement" and "Reason"
To get a solid proof, you have to make a statement and give geometric reasons that prove the statement true. Under the statement column, write a statement such as angle ABC = angle DEF. In the reason column, write evidence that supports the statement. If the reason has been given as a clue to the question, write 'provided by the question'. If not, write a theorem that proves the statement.
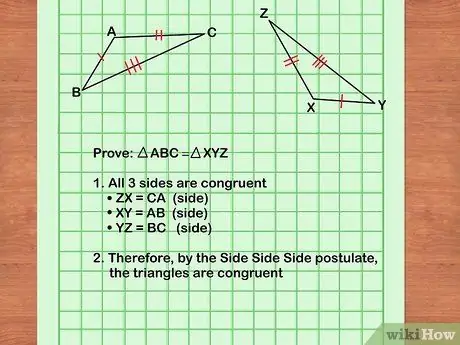
Step 5. Determine which theorem is appropriate for the proof
There are many theorems in geometry that you can use as proofs. Many characteristic triangles, intersecting and parallel lines, and circles are used as the basis for these theorems. Determine what geometric shape you are working on and find a shape that can be used in the proof process. Check previous proofs to detect similarities. This article cannot write down all the geometric theorems, but below are some of the most important triangular theorems:
- Two or more congruent triangles will have congruent side lengths and corresponding angles. In English, this theorem is shortened to CPCTC (Corresponding Parts of the Congruent Triangle are Congruent)
- If the lengths of the three sides of one triangle are equal to the lengths of the three sides of another triangle, the two triangles are congruent. In English, this theorem is called SSS (side-side-side).
- Two triangles are congruent if they have two sides that are the same length and one angle that is the same size. In English, this theorem is called SAS (side-angle-side).
- Two triangles are congruent if they have two equal angles and one side that is the same length. In English, this theorem is called ASA (angle-side-angle).
- If two or more triangles have the same angles, it means that the triangles are similar, but not necessarily congruent. In English, this theorem is called AAA (angle-angle-angle).
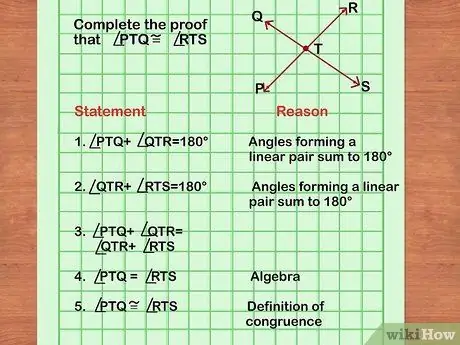
Step 6. Make sure you follow rational steps
Write an outline sketch of your proof. Write down each reason behind each step. Add question clues in the steps that are relevant to the instructions. Don't just write down all the instructions at the beginning of the proof. Rearrange the proof steps if necessary.
The more proofs you do, the easier it will be for you to set the proof steps correctly

Step 7. Write the conclusion on the last line
The last step should complete your proof, but this last step still requires justification. After you finish the proof, re-read it and make sure there are no holes in your reasoning. Once you are sure that your proof is correct, write QED in the lower right corner to emphasize that your proof is complete.
Tips
- LEARN EVERY DAY. Reread today's notes, yesterday's notes, and the materials you have studied previously so you don't forget the propositions/theorems, definitions or symbols/notations.
- Read websites and videos about concepts you don't understand.
- Prepare reading cards with formulas to help you remember and read them again.
- Ask for the phone numbers and email addresses of some friends in your geometry class so they can help out while you study at home.
- Take classes in the previous short semester so you don't have to work too hard in the regular school year.
- Do meditation. This can help you.
Warning
- Don't procrastinate
- Don't try to learn all the material in a short time






