- Author Jason Gerald [email protected].
- Public 2024-01-02 02:28.
- Last modified 2025-01-23 12:04.
Completing squares is a useful technique to help you put quadratic equations into a neat form, which makes them easy to see or even solve. You can complete squares to build more complex quadratic formulas or even solve quadratic equations. If you want to know how to do it, follow these steps.
Step
Part 1 of 2: Converting Ordinary Equations to Quadratic Functions
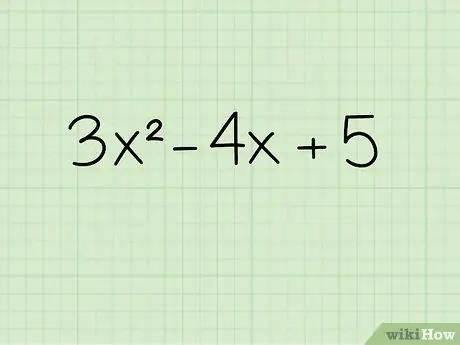
Step 1. Write down the equation
Suppose you want to solve the following equation: 3x2 - 4x + 5.
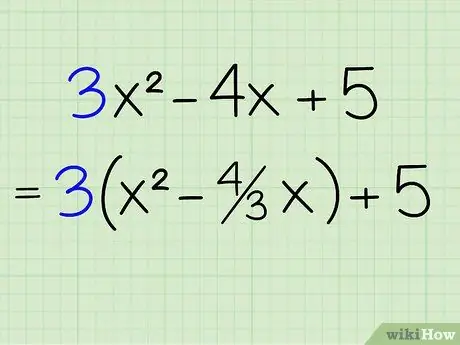
Step 2. Take out the coefficients of the quadratic variables from the first two parts
To get the number 3 out of the first two parts, just take the number 3 out and put it outside the brackets, dividing each part by 3. 3x2 divided by 3 is x2 and 4x divided by 3 is 4/3x. So, the new equation becomes: 3(x2 - 4/3x) + 5. The number 5 remains outside the equation because it is not divided by the number 3.
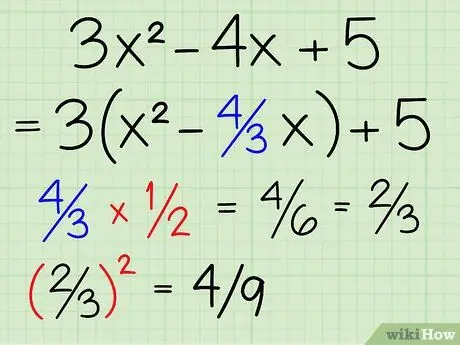
Step 3. Divide the second part by 2 and square it
The second part or what is known as b in the equation is 4/3. Divide by two. 4/3 2, or 4/3 x 1/2, equals 2/3. Now, square this section by squaring the fraction's numerator and denominator. (2/3)2 = 4/9. Write it down.

Step 4. Add and subtract these parts from the equation
You'll need this extra part to get the equation back to a perfect square. However, you have to subtract them from the rest of the equation to add them up. Although, it looks like you're going back to your original equation. Your equation looks like this: 3(x2 - 4/3 x + 4/9 - 4/9) + 5.

Step 5. Remove the part you subtracted from the brackets
Since you have a coefficient of 3 outside the brackets, you can't just output -4/9. You have to multiply it by 3 first. -4/9 x 3 = -12/9, or -4/3. If you have a coefficient of 1 in the x. section2, then you can skip this step.
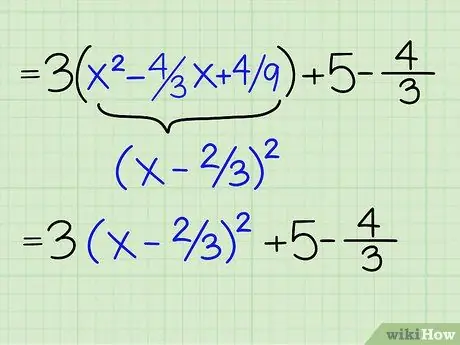
Step 6. Change the part in the brackets to a perfect square
Now, there are 3(x2 -4/3x +4/9) in brackets. You've already tried to get 4/9, which is actually another way to complete the square. So you can rewrite it as: 3(x - 2/3)2. All you have to do is divide the second half and eliminate the third. You can check your work by multiplying it and producing the first three parts of the equation.
-
3(x - 2/3)2 =

Complete the Square Step 6Bullet1 - 3(x - 2/3)(x -2/3) =
- 3[(x2 -2/3x -2/3x + 4/9)]
- 3(x2 - 4/3x + 4/9)

Step 7. Combine the constants
Now there are two constants or numbers that have no variables. Now, you have 3(x - 2/3)2 - 4/3 + 5. All you have to do is add up -4/3 and 5 to get 11/3. You add them by equating the denominators: -4/3 and 15/3, and then adding up the numbers so that you get 11 and leave the denominator 3.
-
-4/3 + 15/3 = 11/3.

Complete the Square Step 7Bullet1
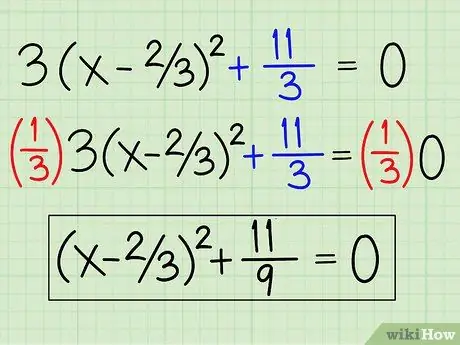
Step 8. Write the equation in quadratic form
You have done. The final equation is 3(x - 2/3)2 +11/3. You can eliminate the coefficient of 3 by dividing both sides of the equation to get (x - 2/3)2 +11/9. You have successfully written the equation into quadratic form, namely a(x - h)2 +k, where k represents a constant.
Part 2 of 2: Solving Quadratic Equations
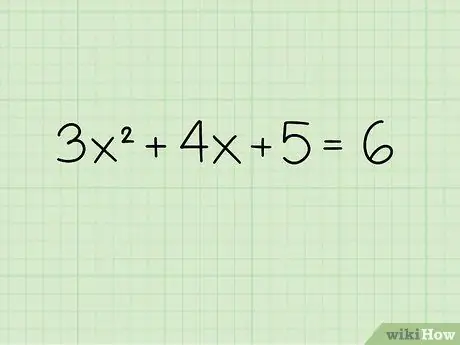
Step 1. Write down the questions
Suppose you want to solve the following equation: 3x2 + 4x + 5 = 6

Step 2. Combine the existing constants and place them on the left side of the equation
A constant is any number that does not have a variable. In this problem, the constant is 5 on the left and 6 on the right. If you want to move 6 to the left, you have to subtract both sides of the equation by 6. The remainder is 0 on the right side (6-6) and -1 on the left side (5-6). The equation becomes: 3x2 + 4x - 1 = 0.
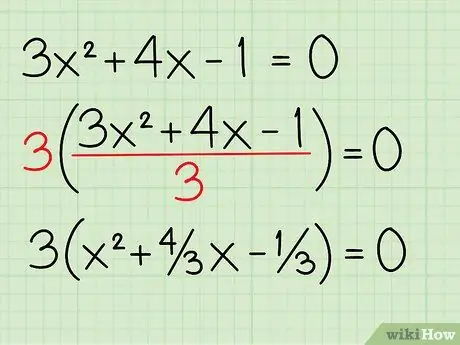
Step 3. Output the coefficient of the quadratic variable
In this problem, 3 is the coefficient of x2. To get the number 3, just take out the number 3, and divide each part by 3. So, 3x2 3 = x2, 4x 3 = 4/3x, and 1 3 = 1/3. The equation becomes: 3(x2 + 4/3x - 1/3) = 0.
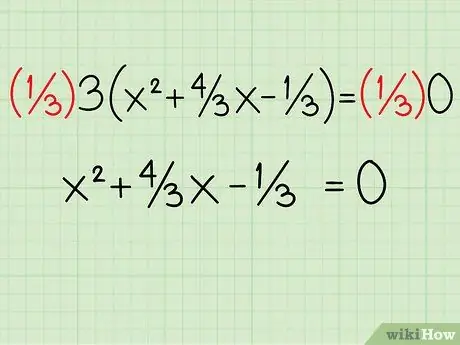
Step 4. Divide by the constant you just extracted
This means that you can remove the coefficient 3. Since you've already divided each part by 3, you can remove the number 3 without affecting the equation. Your equation becomes x2 + 4/3x - 1/3 = 0

Step 5. Divide the second part by 2 and square it
Next, take the second part, 4/3, or part b, and divide it by 2. 4/3 2 or 4/3 x 1/2, equals 4/6 or 2/3. And 2/3 squared to 4/9. If you've squared it, you'll need to write it on the left and right sides of the equation because you're adding a new part. You have to write it on both sides to balance it. The equation becomes x2 + 4/3 x + 2/32 - 1/3 = 2/32
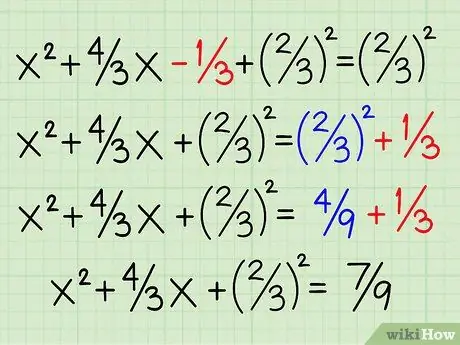
Step 6. Move the initial constant to the right side of the equation and add it to the square of your number
Move the initial constant, -1/3, to the right, making it 1/3. Add the square of your number, 4/9 or 2/32. Find a common denominator to add 1/3 and 4/9 by multiplying the top and bottom fractions of 1/3 by 3. 1/3 x 3/3 = 3/9. Now add 3/9 and 4/9 to get 7/9 on the right side of the equation. The equation becomes: x2 + 4/3 x + 2/32 = 4/9 + 1/3 then x2 + 4/3 x + 2/32 = 7/9.
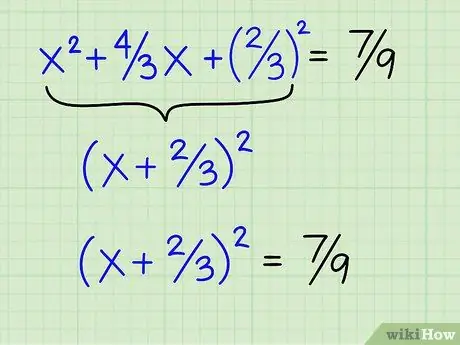
Step 7. Write down the left side of the equation as a perfect square
Since you've already used the formula to find the missing piece, the hard part has been skipped. All you have to do is put x and half the value of the second coefficient in parentheses and square it, for example: (x + 2/3)2. Note that factoring a perfect square will yield three parts: x2 + 4/3 x + 4/9. The equation becomes: (x + 2/3)2 = 7/9.
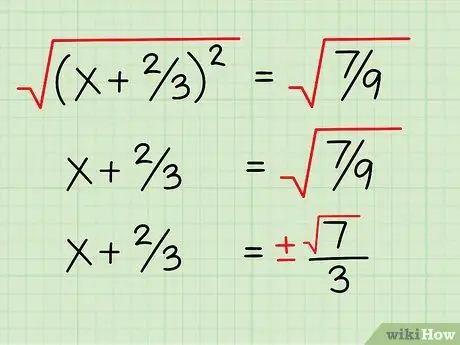
Step 8. Square root of both sides
On the left side of the equation, the square root of (x + 2/3)2 is x + 2/3. On the right side of the equation, you will get +/- (√7)/3. The square root of the denominator, 9, is 3, and the square root of 7 is 7. Remember to write +/- because the square root can be positive or negative.

Step 9. Move the variables
To move the variable x, just move the constant 2/3 to the right side of the equation. Now, you have two possible answers for x: +/- (√7)/3 - 2/3. These are your two answers. You can leave it alone or find the value of the square root of 7 if you have to write an answer without a square root.
Tips
- Make sure to write +/- in the appropriate place, otherwise you will only get one answer.
- Even after you know the quadratic formula, practice completing the square regularly, either by proving the quadratic formula or solving some problems. That way, you won't forget the method when you need it.






