- Author Jason Gerald [email protected].
- Public 2024-02-01 14:11.
- Last modified 2025-06-01 06:05.
Have you ever left a bottle of water in the hot sun for a few hours and heard a slight "hissing" sound when you opened it? This is due to a principle called vapor pressure. In chemistry, vapor pressure is the pressure exerted by the walls of a closed container when the chemical substance in it evaporates (turns into a gas). To find the vapor pressure at a given temperature, use the Clausius-Clapeyron equation: ln(P1/P2) = (ΔHsteam/R)((1/T2) - (1/T1)).
Step
Method 1 of 3: Using the Clausius-Clapeyron Equation
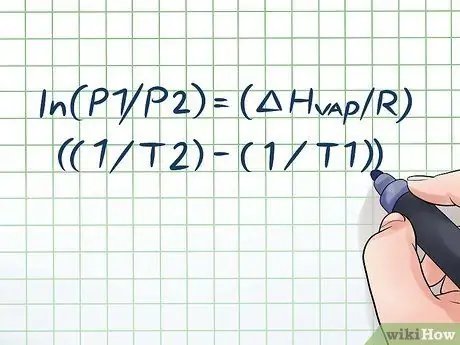
Step 1. Write down the Clausius-Clapeyron equation
The formula used to calculate vapor pressure with the change in vapor pressure over time is called the Clausius-Clapeyron equation (named after the physicists Rudolf Clausius and Benoît Paul mile Clapeyron.) This is basically the formula you will need to solve most types of problems. Vapor pressure questions are often found in physics and chemistry classes. The formula is like this: ln(P1/P2) = (ΔHsteam/R)((1/T2) - (1/T1)). In this formula, the variables represent:
-
Hsteam:
The enthalpy of vaporization of a liquid. This enthalpy can usually be found in the table at the back of the chemistry textbook.
-
R:
The real/universal gas constant, or 8.314 J/(K × Mol).
-
Q1:
The temperature at which the vapor pressure is known (or initial temperature).
-
T2:
The temperature at which the vapor pressure is unknown/wanted to be found (or the final temperature).
-
P1 and P2:
Vapor pressure at temperatures T1 and T2, respectively.

Step 2. Enter the variables you know
The Clausius-Clapeyron equation looks complicated because it has a lot of different variables, but it's actually not that difficult if you have the right information. Most basic vapor pressure problems will write down two values of temperature and one value of pressure or two values of pressure and one value of temperature - once you figure that out, solving this equation is very easy.
- For example, say that we are told that we have a container full of liquid at 295 K whose vapor pressure is 1 atmosphere (atm). Our question is: What is the vapor pressure at 393 K? We have two temperature values and one pressure value, so we can find another pressure value using the Clausius-Clapeyron equation. By plugging in our variables, we get ln(1/P2) = (ΔHsteam/R)((1/393) - (1/295)).
- Note that, for the Clausius-Clapeyron equation, you must always use the temperature value Kelvin. You can use any pressure value as long as the values for P1 and P2 are the same.

Step 3. Enter your constants
The Clausius-Clapeyron equation has two constants: R and Hsteam. R always equals 8.314 J/(K × Mol). However, Hsteam (enthalpy of vaporization) depends on the substance whose vapor pressure you are looking for. As noted above, you can usually find the values of Hsteam for various substances at the back of a chemistry or physics textbook, or online (as, for example, here.)
-
In our example, suppose our liquid is pure water.
If we look in the table the values of Hsteam, we find that Hsteam pure water is about 40.65 KJ/mol. Since our H value is in joules, and not kilojoules, we can convert it to 40,650 J/mol.
- Plugging in our constants, we get ln(1/P2) = (40,650/8, 314)((1/393) - (1/295)).
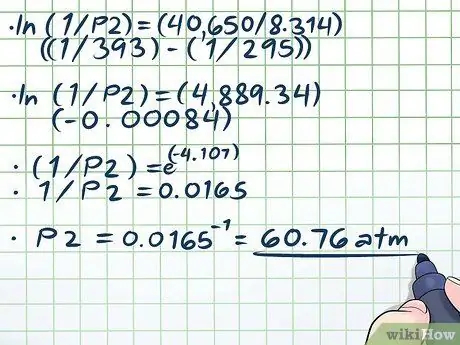
Step 4. Solve the equation
Once you've included all the variables in the equation except the one you're looking for, proceed to solving the equation according to the rules of ordinary algebra.
-
The only difficult part of solving our equation (ln(1/P2) = (40,650/8, 314)((1/393) - (1/295))) is resolving the natural log (ln). To remove the natural log, just use both sides of the equation as exponents for the mathematical constant e. In other words, ln(x) = 2 → eln(x) = e2 → x = e2.
- Now, let's solve our equation:
- ln(1/P2) = (40,650/8, 314)((1/393) - (1/295))
- ln(1/P2) = (4889, 34)(-0, 00084)
- (1/P2) = e(-4, 107)
- 1/P2 = 0.0165
-
P2 = 0.0165-1 = 60, 76 atm.
This makes sense - in a closed container, raising the temperature to almost 100 degrees (to almost 20 degrees above the boiling point) will produce a lot of steam, increasing the pressure rapidly.
Method 2 of 3: Finding Vapor Pressure with Dissolved Solution
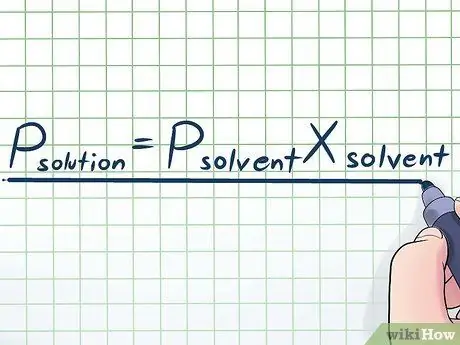
Step 1. Write down Raoult's Law
In real life, we rarely work with a pure liquid - usually, we work with a liquid that is a mixture of several different substances. Some of the most commonly used mixtures are made by dissolving a small amount of a certain chemical called a solute in many chemicals called a solvent to make a solution. In these cases, it is useful to know an equation called Raoult's Law (named after the physicist François-Marie Raoult), which is written like this: Psolute=PsolventXsolvent. In this formula, the variables represent;
-
Psolute:
Vapor pressure of the entire solution (all the elements combined)
-
Psolvent:
Solvent vapor pressure
-
Xsolvent:
Mole fraction of solvent
- Don't worry if you don't know terms like mole fraction - we'll explain them in the next few steps.

Step 2. Determine the solvent and solute in your solution
Before you can calculate the vapor pressure of a mixed liquid, you must identify the substances you are using. As a reminder, a solution is formed when a solute dissolves in a solvent - the chemical that dissolves is always called the solute, and the chemical that makes it dissolve is always called the solvent.
- Let's work using the simple examples in this section to illustrate the concepts we discuss. For our example, let's say we want to find the vapor pressure of sugar syrup. Traditionally, sugar syrup is water-soluble sugar (1:1 ratio), so we can say that sugar is our solute and water is our solvent.
- Note that the chemical formula for sucrose (table sugar) is C12H22O11. This chemical formula will be very important.
Step 3. Find the temperature of the solution
As we saw in the Clausius Clapeyron section above, the temperature of a liquid will affect its vapor pressure. Generally, the higher the temperature, the greater the vapor pressure - as the temperature rises, more of the liquid will evaporate and form vapor, increasing the pressure in the container.
In our example, let's say the temperature of the sugar syrup at this point is 298 K (about 25 C).
Step 4. Find the vapor pressure of the solvent
Chemical reference materials usually have vapor pressure values for many commonly used substances and compounds, but these pressure values are usually only valid if the substance has a temperature of 25 C/298 K or its boiling point. If your solution has one of these temperatures, you can use the reference value, but if not, you'll need to find the vapor pressure at that temperature.
- The Clausius-Clapeyron can help - use a reference vapor pressure and 298 K (25 C) for P1 and T1 respectively.
- In our example, our mixture has a temperature of 25 C, so we can easily use our easy reference table. We know that at 25 C, water has a vapor pressure of 23.8 mm HG

Step 5. Find the mole fraction of your solvent
The last thing we need to do before we can solve this is to find the mole fraction of our solvent. Finding the mole fraction is easy: just convert your compounds to moles, then find the percentage of each compound in the total number of moles in the substance. In other words, the mole fraction of each compound is equal to (moles of compound)/(total number of moles in substance).
-
Suppose our recipe for sugar syrup uses 1 liter (L) of water and 1 liter of sucrose (sugar).
In this case, we must find the number of moles of each compound. To do this, we'll find the mass of each compound, then use the molar mass of the substance to convert it to moles.
- Mass (1 L of water): 1,000 grams (g)
- Mass (1 L of raw sugar): Approx. 1,056, 8 g
- Moles (water): 1,000 grams × 1 mol/18.015 g = 55.51 mol
- Moles (sucrose): 1,056, 7 grams × 1 mol/342.2965 g = 3.08 moles (note that you can find the molar mass of sucrose from its chemical formula, C12H22O11.)
- Total moles: 55.51 + 3.08 = 58.59 mol
- Mole fraction of water: 55, 51/58, 59 = 0, 947
Step 6. Finish
Finally, we have everything we need to solve our Raoult's Law equation. This part is very simple: just plug in your values for the variables in the simplified Raoult's Law equation at the beginning of this section (Psolute = PsolventXsolvent).
- Entering our values, we get:
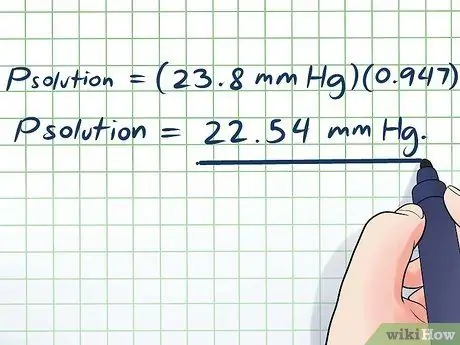
- Psolution = (23.8 mm Hg)(0, 947)
-
Psolution = 22.54 mm Hg.
The result makes sense - in mole terms, there's very little sugar dissolved in a lot of water (though in real-world terms, both ingredients have the same volume), so the vapor pressure will only decrease slightly.
Method 3 of 3: Finding Vapor Pressure in Special Cases

Step 1. Be careful with Standard Temperature and Pressure conditions
Scientists often use a set of temperature and pressure values as an easy-to-use “standard.” These values are called Standard Temperature and Pressure (or STP). Vapor pressure problems often refer to STP conditions, so it is important to remember these values. STP values are defined as:
- Temperature: 273, 15 K / 0 C / 32 F
- Pressure: 760 mm Hg / 1 atm / 101, 325 kilopascals

Step 2. Rearrange the Clausius-Clapeyron equation to find the other variables
In our example in Part 1, we saw that the Clausius-Clapeyron equation is very useful for finding the vapor pressure for pure substances. However, not all questions will ask you to look for P1 or P2 - many will ask you to find the temperature value or sometimes even the H value.steam. Fortunately, in these cases, getting the answer right is simply a matter of rearranging the equation so that the variables you want to solve are separate on one side of the equals sign.
- For example, say we have an unknown liquid with a vapor pressure of 25 torr at 273 K and 150 torr at 325 K, and we want to find the enthalpy of vaporization of this liquid (ΔHsteam). We can solve it like this:
- ln(P1/P2) = (ΔHsteam/R)((1/T2) - (1/T1))
- (ln(P1/P2))/((1/T2) - (1/T1)) = (ΔHsteam/R)
- R × (ln(P1/P2))/((1/T2) - (1/T1)) = Hsteam Now, we enter our values:
- 8, 314 J/(K × Mol) × (-1, 79)/(-0, 00059) = Hsteam
- 8, 314 J/(K × Mol) × 3,033, 90 = Hsteam = 25,223, 83 J/mol

Step 3. Calculate the vapor pressure of the solute when the substance produces vapor
In our Raoult Law example above, our solute, sugar, does not exert any pressure on its own at normal temperatures (think - when was the last time you saw a bowl of sugar evaporate in your upper cupboard?) However, when your solute did evaporate, this will affect your vapor pressure. We account for this by using a modified version of Raoult's Law equation: Psolution = (PcompoundXcompound) The symbol sigma (Σ) means that we only need to add up all the vapor pressures of the different compounds to get our answer.
- For example, say we have a solution made of two chemicals: benzene and toluene. The total volume of the solution is 12 milliliters (mL); 60 mL benzene and 60 mL toluene. The temperature of the solution is 25°C and the vapor pressures of each of these chemicals at 25°C are 95.1 mm Hg for benzene and 28.4 mm Hg for toluene. With these values, find the vapor pressure of the solution. We can do this as follows, using standard density, molar mass, and vapor pressure values for our two chemicals:
- Mass (benzene): 60 mL = 0.060 L × 876.50 kg/1,000 L = 0.053 kg = 53 g
- Mass (toluene): 0.060 L × 866, 90 kg/1,000 L = 0.052 kg = 52 g
- Mol (benzene): 53 g × 1 mol/78, 11 g = 0.679 mol
- Moles (toluene): 52 g × 1 mol/92, 14 g = 0.564 mol
- Total moles: 0.679 + 0.564 = 1.243
- Mole fraction (benzene): 0.679/1, 243 = 0.546
- Mole fraction (toluene): 0.564/1, 243 = 0.454
- Solution: Psolution = PbenzeneXbenzene + PtolueneXtoluene
- Psolution = (95.1 mm Hg)(0, 546) + (28.4 mm Hg)(0, 454)
- Psolution = 51.92 mm Hg + 12.89 mm Hg = 64, 81 mm Hg
Tips
- To use the Clausius Clapeyron equation above, temperature must be measured in Kelvin (written as K). If you have the temperature in Celsius, then you must convert it using the following formula: Tk = 273 + Tc
- The methods above can be used because the energy is exactly proportional to the amount of heat applied. The temperature of the liquid is the only environmental factor that affects the vapor pressure.






