3 Ways to Convert Units

2024 Author: Jason Gerald | [email protected]. Last modified: 2024-01-19 22:11

With different measurement systems in the world, knowing how to convert units can help you. You need to understand how to calculate fractions if you don't use the metric system. For each measurement system you use, always be careful to write down the units at each step to preserve your results.

Step

Method 1 of 3: Converting Units

Step 1. Compare the two units

The two units being compared must measure the same thing. For example, in the question " convert 2 inches to centimeters", both inches and centimeters measure length. If your units measure two different things (such as length and weight), you cannot convert the two units.

• Many people are often confused about length, area, and volume, but they are three different things. Remember that "square" or "²" means area, while "cubic" or "³" means volume.
• You can also write an example like this: 2 in. = ? cm.

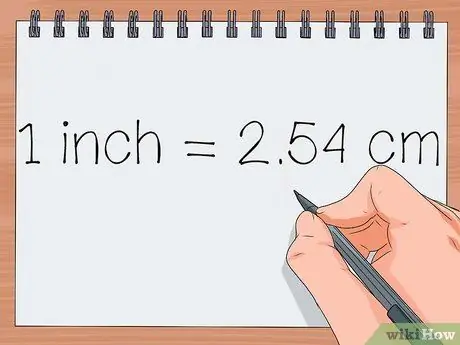
Step 2. Check the unit conversion system

Before you calculate, you need to know the difference between the existing units and the others. If you find a conversion that has many decimal places, round to the nearest number. If you don't know which number to round, round the second or third number.

For example, if you need to convert 2 inches to centimeters, you need to know that 1 inch = 2.54 centimeters.

Step 3. Write the conversion as a fraction

Write down the conversion as a fraction, including the units. Put the starting unit at the bottom (the divisor) and the unit you want at the top of the fraction (the numerator).

For example, write ^{2.54 cm}/_{1 in.}. You can read it like: "2.54 centimeters per inch".

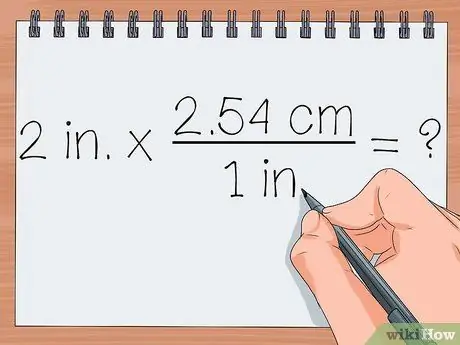
Step 4. Write a multiplication problem with the initial numbers and fractions that have been made

Multiplying these two numbers will give you the answer. To do this, start by writing a multiplication problem with the units after the number.

• 2 in. x ^{2.54 cm}/_{1 in.} = ?

Step 5. Solve the multiplication problem

It's important to keep your count. Each unit in the problem must always be present at every step.

• 2 in. x ^{2.54 cm}/_{1 in.}
• = ^{(2 in x 2.54 cm)}/_{1 in.}
• = ^{(5.08 in. x cm.)}/ _in.

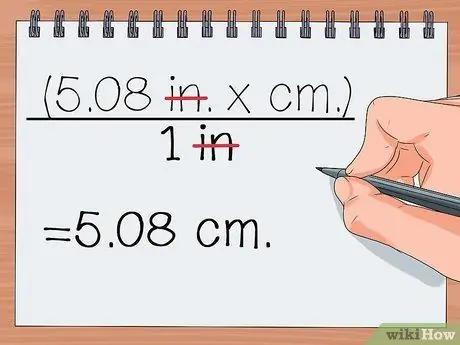
Step 6. Delete the units that appear at the top and bottom of the fraction

If there are units that are the same at the top and bottom of the fraction, cross them out. The remaining units must be the units you are looking for.

• ^{(5.08 in. x cm.)}/_in.

• = 5.08 cm.

  

  Step 7. Fix the calculation error

  If no units are deleted, start the calculation from scratch and try again. You may have written the wrong fraction at the start of the calculation.

  For example, if you were to multiply 2 inches x (1 in. / 2.54 cm), your answer would be "in. x in. / cm" which doesn't make sense. If you reverse the existing fraction, the inches will be erased. Therefore, start again with 2 inches x (2.54 cm / 1 in.)

  Method 2 of 3: Converting Values with Multiple Values

  

  Step 1. Write down the problem you want to solve

  Make sure the unit you want to find and write it down in a math problem. As an example:

  • If a bicycle is moving 10 miles per hour, how many feet does it cover in one minute?
  • Write this problem like "10 miles / hour = ? feet / minute" or " 10 miles/hour = ? feet / min".

  

  Step 2. Find the conversion for a unit

  Remember, you can only convert 2 units that measure the same thing. In this example, there are units that measure length (miles and feet) and units that measure time (hours and minutes). Start with one pair of units and look for conversions between the two units.

  • As an example, 1 mile = 5,280 feet.

  

  Step 3. Multiply your number by the conversion fraction

  As explained in the section above, you can write conversions as fractions so you can delete the same units. Be sure to include each unit in your calculations.

  • ^{10 miles} / _h) x ^{5280 feet} / _miles
  • = ^{52800 miles x feet} / _{hours x miles}

  

  Step 4. Delete the same units

  One of your units will be at the top and bottom of the fraction, so you can cross out the unit. You're still not done, but you're getting closer to the answer.

  • ^{52800 miles x feet} / _{hours x miles}
  • = ^{52800 feet} / _o'clock

  

  Step 5. Multiply the problem by the conversion fraction in the same way

  Select the unit that has not been converted and write the conversion as a fraction. Remember to set the form of the fraction, so that you can cross out the units when multiplying.

  • In this example, you still need to convert hours to minutes. 1 hour = 60 minutes.
  • Now, you have 52800 feet/hour. Since the hour is still below the fraction, use a new fraction with the hour above the fraction: 1 hour / 60 minutes.
  • ^{52800 feet} / _o'clock x ^{1 hour} / _{60 min}
  • = ^{880 feet x hour} / _{hour x min}

  

  Step 6. Delete the same units

  The same units must be crossed out, just like what was done before.

  • ^{880 feet x hour} / _{hour x min}
  • = ^{880 feet} / _min

  

  Step 7. Repeat the above steps until all existing units have been converted

  If the answers are already with the units you want then you are done with the calculations. If not, try to convert to a different unit using the same method.

  • If you are familiar with this method, you can write the entire conversion on one line. For example, you can solve problems like this:
  • ^{10 miles}/_o'clock x ^{5280 feet}/_miles x ^{1 hour}/_{60 min}
  • =^{10 miles}/_o'clock x ^{5280 feet}/_miles x ^{1 hour}/_{60 min}
  • = 10 x 5280 feet x ¹/_{60 min}
  • = 880 ft/min.

  Method 3 of 3: Converting with the Metric System

  

  Step 1. Get to know the metric system

  The metric system, also known as the decimal system, is a system designed to easily convert units. To convert one metric unit to another, you only need to use a whole number, such as 10, 100, 1000, etc.

  

  Step 2. Identify the unit prefix

  Metric units of measurement use a prefix to indicate the size of an existing measurement. Although the examples given are in units of weight, all metric units use the same prefix. In the example, the prefix will be italicized, but you can use a conversion with the frequently used prefix, which is printed thick.

  • kilo grams = 1000 grams
  • hectograms = 100 grams
  • deca gram = 10 gram
  • grams = 1 gram
  • deci gram = 0.1 gram (one tenth)
  • inches gram = 0.01 gram (one per hundred)
  • milli gram = 0.001 gram (one per thousand)

  

  Step 3. Use prefixes in conversions

  If you know the unit prefix to use, you don't have to look through the list of prefixes every time you convert units. The unit prefix above has indicated the conversion value. As an example:

  • To convert kilometers to meters: kilo means 1000 then 1 kilometer = 1000 meters.
  • To convert grams to milligrams: milli means 0.001 then 1 milligram = 0.001 gram.

  

  Step 4. Move the decimal point instead of having to do the calculation

  Using metric conversions, you can skip all the calculation steps as above. Multiplying a number by 10 is the same as moving the decimal point to the left. Here's an example of how to use this:

  • Problem: convert 65.24 kilograms into grams.
  • 1 kilogram = 1000 grams. Count the number of zeros, there are three. Therefore, you must multiply by 10 three times or you can move the decimal point to the right three times.
  • 65.24 x 10 = 652.4 (multiplied once)
  • 652.4 x 10 = 6524 (twice)
  • 6524 x 10 = 65240 (three times)
  • The answer is 65240 grams.

  

  Step 5. Practice with more difficult questions

  You will find it more difficult when you convert prefixed units to other prefixed units. The easiest way to solve this problem is to convert the base units (without the prefix) first, then convert them into the desired units. As an example:

  • Problem: convert 793 milliliters to decalliters.
  • If there are three zeros then move the decimal point to the left three times. (Remember, move the dot to the left when dividing.)
  • 793 milliliters = 0.793 liters
  • 10 liters = 1 decaliter then 1 liter = 0.1 decaliter. There is one zero so move the decimal point to the left once.
  • 0.793 liters = 0.0793 decalliter.

  

  Step 6. Check your answers

  The mistake that is often made is that it is wrong to multiply and it should divide, or vice versa. When you have got your final answer, check the result of the answer:

  • If you convert to larger units, your number should be smaller (same as when converting 12 inches to 1 foot).
  • If you convert to smaller units, your number should be larger (same as when converting 1 foot to 12 inches).
  • If the results don't match this answer, check your workflow.